

However, there are many other relationships that lead to negative correlation, so it is not correct to say that negative correlation always indicates an inverse relationship.Īs some commentators have pointed out, the word "inverse" can be used in its strict mathematical sense, or in a broader sense that refers generally to relationships that are "opposing" in some broad way. In the case of an inverse relationship $y=1/x$ (which is nonlinear), random sampling of these values certainly be negatively correlated (assuming they are both positive $^\dagger$) so it is correct to say that an inverse relationship does lead to negative correlation. In the context of ratio-scale measurement, negative correlation does not properly measure the inverse functional relationship.Ĭorrelation only measures the linear component of a statistical relationship, so if there is a nonlinear statistical relationship, it may still show up as correlation, but the correlation will not fully describe the relationship. Short answer: You don't have to eat your words.
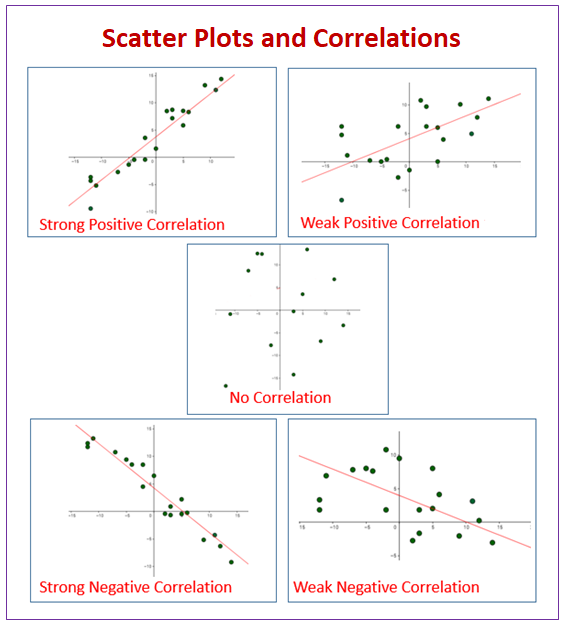
Negative relationships imply additive inverses not proportional (i.e., multiplicative) inverses, and use of the word inverse in two separate contexts simultaneously is ill advised. So, do I have to eat my words? Or can I continue to tell people not to call negative relationships inverse? have the following answers 1) Yes, you are correct, and should not (never mind cannot) eat your words. In that light, then, we can state that the phrase "A negative correlation means that there is an inverse relationship between two variables - when one variable decreases, the other increases." is 1) gibberish of the hand-waving type, that 2) uses the word "inverse" improperly, and which when cleaned up by replacing the all of the improper language could read "A negative correlation means that the normalized covariance is negative," furthermore 3) A negative correlation does not imply monotonicity between discrete random variables, the admixture of continuous and discrete parameter types notwithstanding, and if not totally incorrect it is a stretch to define a correlation via an ordinary least squares in $y$ linear regression model that would have monotonicity.
Now note, the inverse of monotonically increasing is not monotonically decreasing, which demonstrates what the semantic problem is. The unambiguous terminology for "as $x$ increases, $y$ increases" is monotonically increasing, and, to affirm that this is not local, the term strictly monotonically increasing is used, the inverse of which is then monotonically non-increasing and not strictly monotonically decreasing. For it to be an inverse, it would have to be an inverse of some algebraic operation, and the reason for using it in this context is otherwise, namely that it is inverse hand-waving of "as $x$ increases, $y$ increases type," and hand-waving is also not a defined algebraic procedure. The OP's question is: Is it correct to refer to a negative correlation as an 'inverse correlation'? The answer is no, correlation is intransitive, that is, given a correlation one cannot invert the procedure. What operation is an inverse of what other operation depends on which algebraic procedure is being used, for example, subtraction is inverse addition, division is inverse multiplication, deconvolution is inverse convolution, a matrix inverse is the inverse of an invertible matrix, an inverse Laplace transform is the inverse of a Laplace transform, and so on. In general, to keep the word inverse from causing confusion, all that need be done is to say inverse _ <- what and fill in the blank. Although true for definite positive inverse proportionality, this has the disadvantage of not being unique, as a negative slope direct proportionality has that same property. The concept of inverse proportionality is often approached at the beginner level by hand-waving in this fashion in this equation as $x$ increases, $y$ decreases. Similarly, it would be rare to use the phrase directly proportional to the negative of something, as it is easier to grasp a negative slope, and rework a phrase to accommodate that. More exact phraseology would be directly proportional and inversely proportional. That is inexact language use, of the type often called hand waving, with the advantage of helping students uncomfortable with the concept of proportionality to grasp the essentials of proportionality without using the word. In physics, more so than other things, one has occasion to say directly related and inversely related when speaking of proportional relationships.


 0 kommentar(er)
0 kommentar(er)
